The following is online calculator for second order active low pass filter. In this filter there are two RC filters with the first filter made up of the R1 and C1 and the second filter made up of R2 and C2. In the calculator we have assumed resistors R1 and R2 to be equal and the capacitors C1 and C2. For Butterworth response the pass gain (AF) must be 1.586.
Second Order Active LPF Calculator

Formula Used:
\( let \; R=R_1=R_2, \\ C=C_1=C_2, \\ R = \frac{1}{2 \pi f_c C}, \\ R_F = R_3(A_F - 1) \)
\( let \; R=R_1=R_2, \\ C=C_1=C_2, \\ R = \frac{1}{2 \pi f_c C}, \\ R_F = R_3(A_F - 1) \)
Notes on 2nd Order Active Low Pass Filter Calculator
- Example Worked Out
The tutorial Active 2nd order LPF on breadboard shows how to use this calculator and build and test the filter on breadboard.
- Cutoff frequency
\[f_c=\frac{1}{2 \pi \sqrt{R_1 R_2 C_1 C_2}}\]
In the above calculator we have assumed R1 = R2 = R and C1 = C2 = C. Then the above formula for the cutoff frequency becomes,
\[f_c=\frac{1}{2 \pi R C}\]
- Butterworth Response
For Butterworth response the passband gain must be 1.586
- Capacitor Values
For best result select the capacitor C value in the range 0.001uF and 0.1uF.
- Rolloff
The roll-off of the second order filter is -40dB/decade. This is double of the first order active LPF circuit.
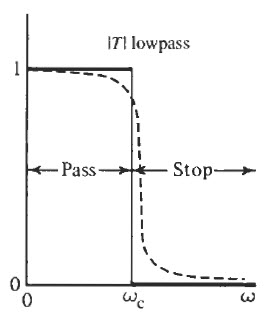
An ideal low pass filter frequency response graph is shown below.
where \(w_C\) is the cutoff frequency.
The above is just ideal graph with instant transition from passband to stopband. A practical filter has smooth transition from passband to stopband with with rolloff. Such practical low pass filter frequency response is shown below.
where \(\alpha\) is the attenuation in dB.
The passband extends from 0 to \(w_p\). In the passband \(\alpha_{max}\) is the maximum attenuation and in the stopband which is the region above \(w_s\) we have minimum attenuation designated as \(\alpha_{min}\). The region between the stopband and passband which extends from \(w_p\) to \(w_s\) is called the transition band.
In the more involved filter design, filter are specified with the parameters: \(\alpha_{max}\), \(\alpha_{min}\), \(w_p\) and \(w_s\). Given these four filter parameters, the problem is to find the attenuation \(\alpha(w)\). This is solved mathematically by using approximation of filter in which the transfer function \(T(s)\) is determined that the attenuation \(\alpha(w)\) satisfies the four parameters. In case of low pass filter the condition are that:
- \(\alpha(w) \leq \alpha_{max}\) when \(w \leq w_p\)
- \(\alpha(w) \geq \alpha_{min}\) when \(w \geq w_s\)
In the above ideal low pass filter response graph we can observe that in the passband the signal are passed through the filter without any attentuation or gain. That is in the passband, |T|=1 when \(\alpha\)=0. But when using active filter this might not be the case because active filter are build using operational amplifier which inserts gain. So when designing low pass active filter with given specification one may need to reduce the insertion gain. That is when active filter is inserted between input and output there is insertion gain and when passive filter in inserted between input and output then there will be insertion loss.
- Other online calculators
- Related filter tutorials
Tags:
filter calculator